“價值投資並不需要什麼高智商，而人們總是想得很複雜，其實這只是複利的倍增而已。”

——沃倫·巴菲特（證券投資教父，前世界首富）

巴菲特認為:投資最大的收益是“時間的複利”。複利是投資者成功的必備利器。短暫的追漲殺跌難成大氣候，世界上眾多成功的投資者，莫不借助於長期穩定的複利的投資手段。巴菲特說:“複利有點像從山上滾雪球，開始時雪球很小，但是當往下滾的時間足夠長，而且雪球粘得適當緊，最後雪球會變得很大很大。

財富增長

要想學投資，先弄懂複利吧。複利就是我們常說的：利滾利

複利到底是什麼呢？為什麼這麼厲害，複利真的能夠實現嗎？

01

故事一：棋盤上的米粒

古時候有個國王非常喜歡下棋，為了感謝國際象棋的發明者，國王答應滿足發明者一個要求。

米粒排布

發明者說：就在棋盤上發一些米粒吧，第一格1粒米，第二格2粒米，第三格4粒米，每一格都是前一格的兩倍，一直到64格。

國王哈哈大笑的滿口答應了，並對發明者說，你真傻，就要這麼一點米粒？發明者回到到：就怕您的國庫沒有這麼多米。

米粒排列

 

經過計算，放滿國際象棋64格需要1844億萬粒米！

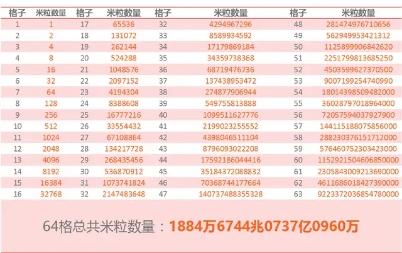
米粒數

相當於當時全世界米粒總數的10倍！

最後，國王的國庫裡根本沒有這麼多的米，而是選擇了其他的方式獎勵發明者。

02

故事二：曼哈頓島

1626年荷蘭人花了大約24美元價值的飾品從印第安人手中藉用曼哈頓島。到2000年1月1日，曼哈頓島的估值為2.5萬億美元。

曼哈頓島

思考：假如印第安人用24美元進行投資能賺多少？

如果當時的印第安人拿著這24美元去投資，按照11%（美國近70年股市的平均投資收益率）的投資收益計算，到2000年能有多少財富。

答案是：24*（1+11%）^（2000-1626+1）≈238萬億美元

相當於曼哈頓島估值的95.2倍！

故事的另外一個版本，曼哈頓島是荷蘭人以價值24美元的飾品從印第安人手中藉的。

並在藉據上註明：歸還此島是，對方要還本付息，年利率為6%，但藉據上並沒有註明利息是單利還是複利計算。

354年後的1980年，雙方當事人的後代告到了法院，請法官判明是非。法官請來了數學家進行了計算，結果使法官大吃一驚。

計算結果

 

單利和復利相差如此之大！

複利是如何計算的？

複利計算公式

 

可能小伙伴們覺得，那些身價動輒上百億的富豪離自己太遠，那麼對於我們普通人而言，在理財中，複利能給我們帶來的好處，究竟有多大呢？

前香港首富李嘉誠，在聊到普通人如何獲得財富時，曾舉過一個例子：

一個人從現在開始，每年投資1.4萬元，如果每年能獲得平均20%的投資回報率，40年後，資產會變成為1億零281萬元。

這個結果沒問題，已經驗證過。

普通人能通過複利獲取什麼？

當然，這個例子中，20%的回報率有些過高了，都快趕上巴菲特的年復合收益率了，大多非專業數投資者很難做到。甚至你會覺得這有些脫離實際。

的確，我也這麼認為，誰能長期保持20%收益呀？太難了~

所以，我決定用一個更為“接地氣”的例子，來算算

普通人做理財，

堅持複利+長期的原則，20年後能積累多少財富?

STEP1:

首先，我們設定一個更加理性化、更為容易達到的年收益率：8%.

香港的儲蓄定投，手頭錢多也可以做信託，都是風險極低並且能比較輕鬆的達到這個收益率。

STEP2:

一個準中產家庭，每年拿出10萬元用於理財，還是可以的，不會影響到日常生活。

即：每年投資10萬元，次年利息复投，堅持投5年，至第21年，資產將增長至216.22萬元。

詳細計算結果如下：

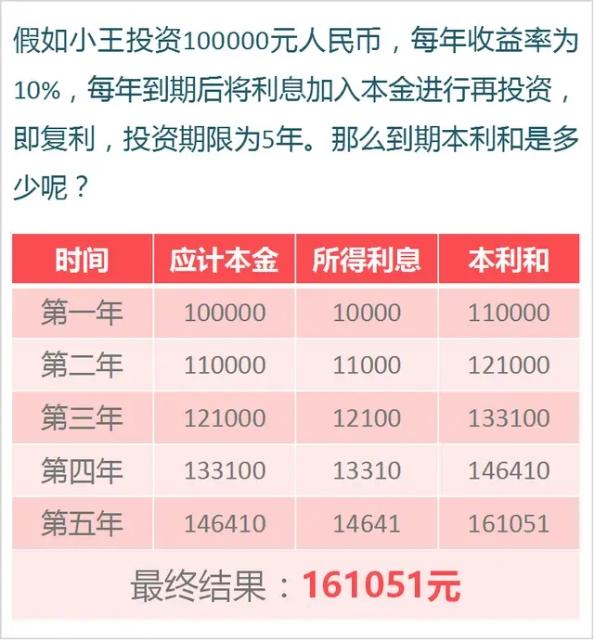
投資複利

 

實際上，第1年的10萬塊，在第10年的時候已經翻了1倍，在第15年的時候翻了2倍，在第19年的時候翻了3.3倍——可以看到，複利的時間越久，越能讓你的資產呈現幾何級的增長。

如果畫出曲線，大致是下面這個樣子：

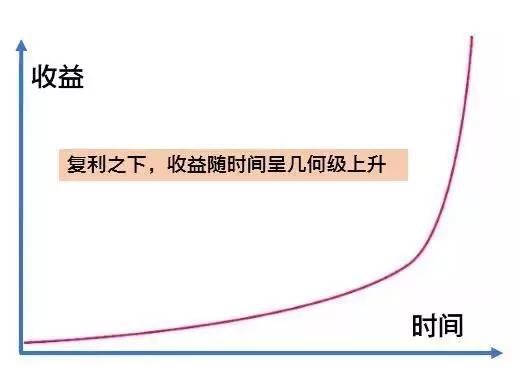
指數增長

 

所以說，即便收益率不太高，只要堅持下來，長此以往，結果依然驚人。

這也就是為什麼，愛因斯坦將復利稱為世界第八奇蹟的同時，更強調了時間的重要性：

“複利完美擴張了時間的價值空間，使得財富的倍增效果無與倫比！”