為什麼學習不僅要結果，更要過程？

兩個人都能解決同一個問題，但他們用的方法可能不同。有些解決問題的方法容易應用到解決其他問題上，另一些方法就不容易。因此，我們不僅要關心問題的解決結果，而且要關心解決問題的方法，不同的方法意味著不同的知覺、記憶，應用了不同的技能和策略。

心理學家卡托納曾經做過一個這樣的實驗。只允許受試者動三根火柴把下圖中的五個方塊變成四個等大的方塊。他給三組受試者不同的指導：

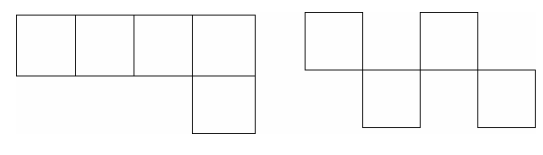
火柴問題（1）機械學習：告訴受試者移動哪幾根火柴，讓他硬記，而不加任何解釋。

（2）給予解釋：告訴受試者其有16根火柴，如果每根都成為方塊的一條邊，那就可以組成四個方塊。在這裡16根火柴之所以能組成五個方塊，是由於有些火柴作了兩個方塊的公用邊。要解決這個問題應使每根火柴只起一條邊的作用。這個解釋容易使人迷惑，因為應該挪動的三根火柴並不是起公用邊作用的，而是起單條邊作用的火柴。但是挪動了這三根起單條邊作用的火柴可以消除起公用邊作用的火柴。

（3）給予暗示：啟發受試者說“因為五個方塊在一起太擠了，所以才使得某些火柴起到雙重功能的作用（公用邊）。要解決這個問題，就要使這些方塊分散開”。

受試者所用的這三種方法都不需要很多的短時記憶。雖然三種方法的策略不同，但受試者最後都能解決問題。

然後，卡托納把問題稍微做了修改，如下圖所示。

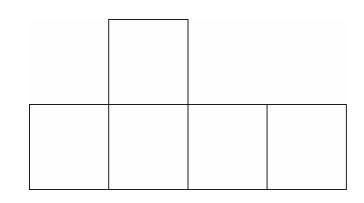
火柴問題的變式在這種情況下，先前用機械學習方法解決問題的受試者，現在就遇到了很大的困難，而用後兩種方法的受試者，特別是用第三種方法的受試者，卻很容易解決問題。

機械學習的方法是無意義的學習，記憶沒有多餘性，學會的內容難以保持。至於為什麼第三種暗示啟發的方法要比第二種解釋的方法效果好，可能是後者告訴了受試者火柴的單功能與雙功能問題，反而把受試者的思路引向火柴的功能本身，而不去注意最後的目標。暗示啟發的方法最有效，當告訴受試者方塊太集中，需要散開，就是說需要破壞原有的結構，移動幾根火柴使各個方塊離開遠一些，這樣就接近達到最後的目標。

用不同的學習方法會得出十分不同的結果。我們不僅要學會解決問題，而且要學會使用較好的方法解決問題。如果一個人總使用機械學習方法，他會認為自己學會了，以後習慣用這種方法，實際上他是很難把知識運用到新的情境中去的。

問題解決的途徑

人在解決問題的時候，可以採取不同的途徑或方法。人們可以用隨機嘗試的方法，經過多次試錯，最後得到答案；也可以根據一些規律，或在經驗中已經證明是行之有效的方法來解決問題，而且把嘗試的次數減到最少。另外還有其他解決問題的方法，下面介紹的就是其中的幾種。

假設—檢驗法

現在以解密碼算術題為例，來說明解決問題所採取的兩種不同的途徑。下面這個密碼題的上、中、下三行各是一個人名：

DONALD
+GERALD
ROBERT

已知：D=5

任務要求:
（1） 把字母換成數字；
（2） 字母換成數字後，下面一行數字答案必須等於第一行與第二行數字之和。

這個問題比較困難，因為解題共有300萬個可能的嘗試，即10!=3×106。如果我們知道了一個線索：D=5，則各種可能的嘗試減為9!=3×105個。

一種解決問題的方法是，每個數字任意給一個英文字母，進行計算，當發生矛盾時就把數字和字母之間的對應關係再做新的安排，重新計算。用這種隨機嘗試的方法需要3×105次才能得到正確答案。

另一種方法是，系統地從右向左，利用解決問題中所得到的知識來做。因為D=5，就可以知道T=0。由於我們知道了T和D的數值，嘗試的範圍就縮小了。最右邊的一列解決後，接著再看其左邊的一列。用這種方法反覆試驗，經過許多組合，可以得出一個正確答案。

然而，以上兩種先提出假設再進行檢驗的方法（假設檢驗法）都不是有效的方法。在實驗室中採用這兩種方法的人往往都失敗了。

選擇性搜索

解決密碼算術題的有效的方法是先找出可能性最少的一列，從中獲得最多的信息；再利用加法中的某些規則去進行推理，從而找到正確答案。這種方法叫作選擇性搜索或啟發式搜索。

所謂可能性最少的那一列，就是限制性最多的那一列。

能夠解答這一問題的受試者幾乎都用了這種方法。在解決這個問題時，受試者的主要思路只有幾條，只利用了6個可能性，而不是用30多萬次的嘗試。由此可見，由於採取了這幾條主要的思路，就可以排除大量的嘗試，達到解決問題的目的。

這種有效的方法就叫作啟發式搜索。

爬山法

爬山法的基本思想是設立一個目標，然後向目標方向運動，逐步逼近目標。這就像爬山一樣，如果在山腳下，要想爬到山頂，就得一點點地往上走，一直走到最高點。有時爬山法得先上矮山頂，然後再下來，重新爬上最高的山頂。因此，爬山法只能保證爬到眼前山上的最高點，而不一定是真正的最高點。

在一些經典的用人或動物做受試者的心理學實驗中，除了設立目標之外，還在目標與受試者之間加入一個障礙，使受試者不能直接達到目標，如下圖所示：

在目標與受試者之間加入障礙

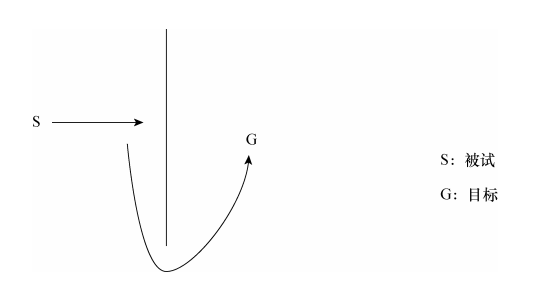
在這種情境下，受試者要花費相當長的時間去克服困難，找到繞過障礙的方法，有時甚至要倒退才能繞過障礙物達到目標。這就相當於在爬山法中經過曲折的途徑而達到最高的山頂。當然，爬山法在我們日常生活中也是有用的方法，不少實際問題都是靠這種方法解決的。

總結以上幾種解決問題的方法，我們看到，初次接觸一個問題的人之所以能夠解決這個問題，就在於他可以把過去已經掌握的一般解決問題的方法應用到新的情境中去。心理學的智力測驗並不是測受試者已經知道的東西，而是測他將過去掌握的一般知識應用到解決測驗的項目中去的能力。

我們通常把不依賴已有的具體知識來解決當前問題的方法稱作弱方法。前面提過的假設檢驗法就是弱方法。用假設檢驗法解決密碼算術題時，任意給每個密碼設想一個數，然後再進行檢驗，這裡並沒有運用已有的具體知識。爬山法也是弱方法。這些方法是最粗糙的方法，其效率是很低的。如果是利用已有的有針對性的知識來解決某個問題，這就是強方法。例如，讓受試者找X、Y的函數關係，如果他沒有微積分知識，就得一點一點地試，使X值逐漸增大，看Y的變化，一直到找到最高點，得出結果。這就是弱方法。如果他已經具備數學方面的知識，那麼就可以利用微積分把最高點定為0，這就是強方法。選擇性搜索是利用過去已有的知識經驗，有針對性地提出假設，然後再進行檢驗得出結論。這是有效的解決問題的方法，是一種強方法。在解決某個問題的時候利用強方法，是非常重要和有效的。

手段目的分析法

人類解決問題有一個很重要的方法，即手段目的分析法(means-end analysis)。這種方法的複雜性在於我們現有的狀態與目標之間會有多種差異，而不是一種差異。我要去聽課，卻忘記帶本子和筆，要解決本子和筆這兩個差異，才能在課堂上記筆記。我發現身上帶著幾角錢，於是就產生了買紙和筆的活動。但是，買了紙後再買筆，錢又不夠用了，這時我就發現自己做錯了，於是又把紙退了，用退了紙的錢去買筆，買過筆再用剩下的錢去買紙。解決問題中出現多種距離和差異的情況是常見的。我們解決了第一步問題，然後再解決第二步問題，可是在解決第二步問題時，第一步問題又出現了。因此，為了更好地運用手段目的分析法解決問題，就需要有解決問題的結構。

例如，玩魔方時，我們可以先把其一面完全變成單色，比如先把第一面變成白色，然後再想辦法把其他幾面分別變成紅的、黃的等等。這裡的問題是，在變第二面時不能破壞第一面；變第三面時不能破壞第一、第二面。我們也可以用手段目的分析法來解決這個問題。使用這種方法我們在變第二面時，可以破壞第一面，但只是暫時的，還要很快地恢復第一面的全白色。事實上，這種一面一面地解決的方法不一定是最好的方法。這是個慢的方法。我們最好能用更簡單的方法，從整體上來考慮如何把魔方恢復為六面單色。為了學會這種整體性的動作，或者說是“宏觀動作”，我們不如買一本魔方解答指南一類的書，從中學會這種“宏觀動作”。這種“宏觀動作”不是原來的一個動作，而是一系列的動作，包括暫時破壞某一面又將其恢復的過程。

這種解魔方的宏觀方法，平時我們就稱其為“計劃”。

心理學教科書中時常引用的畫4條直線通過9個點的問題圖(見下圖)，看起來容易，做起來卻很困難。這個題可採取的搜索樹的分枝並不多，但人們考慮問題時卻往往忽略某種可能性，即為了解決這個問題，解題人所畫的直線一定要超出這9個點所形成的正方形，否則就無法解決。儘管出題的人並沒有限制解題者，也沒有禁止他超越正方形，但解題者卻常常自己限制了自己，他沒有考慮到利用某種算子來解題，因而使問題變得很難。

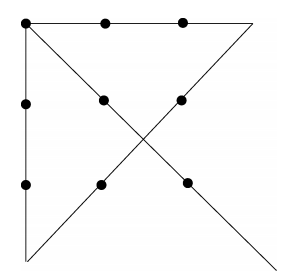
4條直線通過9個點的題解書生和野人的問題也屬於這類問題。題目是這樣的：有三個書生和三個野人走到河邊，河裡只有一條渡船，而且至多只能乘兩人。現在問應該怎樣使用這條船將三個書生和三個野人渡到對岸去。解決這個問題有一個條件，即無論在船上還是在岸邊，書生的人數都不得少於野人，否則書生就要被野人吃掉。解決這道題的方法分如下幾步(見下圖)：

（1）兩個野人先過河。
（2）一個野人划船返回。
（3）然後再過去兩個野人。
（4）一個野人又划船返回。
（5）兩個書生一起過去。
（6）為了進一步解決問題，現在要走關鍵的一步，就是要有一個書生和一個野人划船回來。只有想到這一步，以後各步才能順利進行。

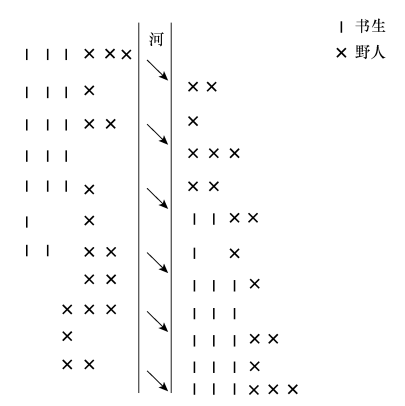
書生與野人過河方法這個問題是不容易解決的。一位大學教授在一刻鍾內也常常解決不了，除非他能認識到，儘管目的是盡量向對岸擺渡更多的人，使他們全部過去，但是也允許兩個人划船回來，問題才容易得到解決。這樣的問題的搜索空間並不太大，關鍵是在第六步兩個人划船回來。由於一般很難想到兩個人划船回來這一步，所以問題就變得很難。

所以，有的問題的困難不在於問題本身，而在於人們思維習慣。 考慮問題時忽略了某種可能性，沒有想到某一種似乎背離目標但實際是接近目標的方法，或者不能很好地把問題形象化都會導致問題變得難以解決。